Correction de l'Examen de Passage - Théorie 2013 - TDI
Dossier 1 (13pts)1. Il s’agit de vérifier les connaissances générales du stagiaire dans le domaine de l’informatique. Le correcteur saura apprécier la pertinence des réponses. (2pts)
2.

a. Représenter la fonction F sur une table de vérité. (1 ,5pt)
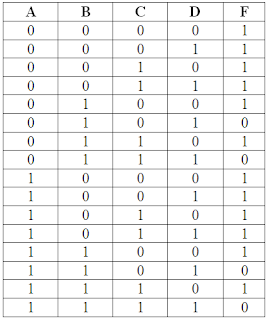
b. Simplifier graphiquement la fonction F. (1,5pt)

Réunir les éléments de la première colonne et de la dernière colonne : ¯B. Puis réunir les éléments de la première ligne et de la dernière ligne :

3. Au parlement, il y a 300 représentants qui tentent de voter une loi. Un vote peut se traduire par l’un des trois cas suivants : Oui, Non et Abstention. Abstention signifie refus de participer au vote.
a. Nombre de résultats coïncide avec le nombre d’applications d’un ensemble ayant 300 éléments (les votants) vers un ensemble de 3 éléments (Oui, Non, Abstention) puisque chaque votant choisira une de ces trois options. Donc le nombre de résultats est égal à 3300. (2pts)
b. D’abord on va compter le nombre de cas favorables. Chaque fois que nous fixons un groupe de 120 représentants parmi les 300 votants qui vont choisir l’option « Oui », nous devrons choisir 120 autres représentants parmi les 180 (=300-120) restants qui vont choisir l’option « Non ». Nous avons donc fixé 240 (=120+120) représentants et donc il nous reste à choisir 60 représentants parmi les 60 (=300-240) restants qui vont « s’abstenir ».

Tous les cas sont équiprobables. Donc, la probabilité est égale au résultat de la division du nombre des cas favorables par le nombre des cas possibles. Donc le résultat cherché est : (2pts)
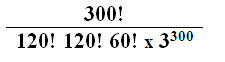
4. Convertir en octal et en décimal les nombres suivants : il est plus simple de passer de la base 16 à la base 2 et puis de cette dernière vers la base 8 :
a. (1001,1)16 = (1 0000 0000 0001,0001 0000)2 = (001 000 000 000 001,000 100)2 = (10001,04)8. (2pt)
(1001,1)16 = (1 * 163 + 1 * 160 + 1 * 16-1)10 = (4097,0625)10
b. (1000)16 = (10000)8 : il suffit de soustraire un du résultat précédent. (2pts)
(0,01)16 = (0,0000 0001)2 = (0,000 000 010)2 = (0,002)8
Donc (1000,01)16 = (10000,002)8
De même, (1000)16 = (4096)10
(0,01)16 = 1 * 16-2 = (0,00390625)10
(1000,01)16 = (4096, 00390625)10
Rappel : le stagiaire doit fournir plus de détails au niveau des calculs. Attribuez la note Zéro (0) si un résultat est fourni directement sans détails.
Dossier 2 (12pts)
Soon...
Dossier 3 (6pts)
a. MCD
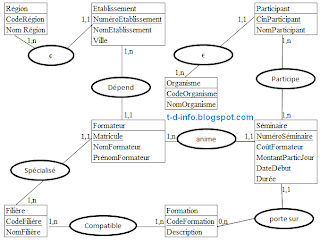
b. MLD

Dossier 4 (9pts)
La solution proposée plus bas, vise surtout à montrer le caractère « récursif » de la méthode ToString.
class Personne { public string Nom, Prenom; public Personne Père, Mère; public Personne(string Nom, string Prenom) { this.Nom = Nom; this.Prenom = Prenom; // Les deux instructions ci-dessous ne sont pas vraiment nécessaires : Pere = null; Mere = null; } public Personne(string Nom, string Prénom, Personne P, Personne M) { this.Nom = Nom; this.Prenom = Prenom; Pere = P; Mere = M; } public string NomComplet() { return Nom + "\t" + Prenom; } public override string ToString() { if (Pere != null) return Pere.ToString() + Environment.NewLine + Pere.NomComplet(); else return ""; } public void affiche() { string ch=ToString(); Console.WriteLine("Cette personne se nomme : " + NomComplet()); if(ch!="") Console.WriteLine("Liste des ancêtres à partir du plus ancien :" + Environment.NewLine + "Nom\tPrénom" + ch); } }
Télécharger la correction de l'examen de passage - Théorie 2013 :
Soon ...
